Biology
Summary
This page explores the intersection of biology, mathematics, and metaphysical concepts through the application of the ABBA equation. It presents biology as a study of life unified by cellular structures and genetic information, linking this to spiritual representations of life forms as embodiments of light. The concept of "form" is central, reflecting how biological morphogenesis shapes organisms and connects to patterns created by vibratory forces in cymatics. The ABBA equation is metaphorically applied to explain various phenomena, from the structure of mycelium networks to the wingbeat frequency of moths, illustrating the interconnectedness and adaptability of life. Furthermore, this page highlights the equation's potential applications in molecular structure design, suggesting its versatility in representing complex interactions, from biological systems to astrophysical and magnetic phenomena. This approach emphasizes the rhythmic, cyclical, and balanced nature of natural processes, encouraging a holistic understanding of the mathematical principles that govern the diversity and adaptability of life.
Introduction
The concept of “form” holds a pivotal role, both in the realm of biology, particularly in the process of morphogenesis, and beyond. In the biological context, morphogenesis signifies the intricate shaping of an organism through embryological procedures that encompass cell differentiation, tissue development, and organ system formation, all orchestrated by the genetic “blueprint” of the potential organism and influenced by environmental conditions. However, the notion of form is not confined to the biological sphere, as evidenced by its presence in the study of cymatics, where vibratory forces give rise to distinct patterns. Form serves as a defining element within which the distortion or LSF (Light, Sound, and Form) framework takes shape, providing the visual characteristics we associate with every plant, tree, or animal. Furthermore, in the natural world, forms can be genetically altered through molecular genetics, enabling molecular scientists to modify features such as flower color in a chrysanthemum, generating hitherto unprecedented expressions and distortions.
The ABBA equation, a mathematical expression with multifaceted interpretations and applications, can be metaphorically related to life as a form. It symbolizes the underlying mathematical order governing patterns and structures in nature, such as the branching of trees or spirals in shells, which are inherent in various life forms. The equation’s focus on oscillatory behavior mirrors the rhythmic and dynamic nature of life, where everything experiences constant change and adaptation. Furthermore, the notion of interconnectedness represented in the ABBA equation aligns with the web of life, where the well-being of one component depends on the health of others within complex ecological systems. Life’s capacity for creative and artistic expression, drawing inspiration from the patterns and rhythms in nature, also resonates with the equation’s connection to the art of weaving. In essence, while the ABBA equation is mathematical, it serves as a metaphorical reminder of the mathematical and rhythmic principles that underlie the diversity, interconnectedness, and creative essence of life itself.
There is an intriguing juxtaposition of the abstract and the organic, the ABBA equation and mycelium offer a fascinating exploration of interconnectedness, adaptability, and the hidden patterns that govern the world around us. On one side, we have the ABBA equation, a mathematical expression with multifaceted applications, symbolizing the elegant precision that underlies mathematical thought. On the other, we dive into the world of mycelium, the complex network of fungal threads that thrives beneath the forest floor, embodying the intricacies of life’s interconnected systems. This exploration unravels the poetic connections between the abstract oscillations of the ABBA equation and the pulsating, adaptive growth of mycelium, underscoring the profound interplay of patterns and rhythms that transcend the boundaries of mathematics and biology.
Example #1: Mushrooms
One way to relate the ABBA equation to mycelium is through the concept of interconnected systems. The ABBA equation hints at the universe operating within a matrix-like structure, emphasizing the interdependence and interactions between its components. In a similar vein, mycelium operates beneath the forest floor in a vast, interconnected network. These fungal threads, which make up the mycelium, function as a biological matrix, connecting trees, plants, and microorganisms. This network enables the exchange of nutrients, water, and information, highlighting the interconnectedness of life.
Complexity and Adaptation:
The ABBA equation’s multifaceted nature and versatility can be metaphorically related to the complexity of mycelium. Fungal mycelium plays a crucial role in nutrient cycling, plant communication, and ecosystem health. It adapts to its surroundings, demonstrating its versatility much like the equation adapts to various applications.
Quantifying Space and Distance of Mushroom Growth
The ABBA equation, [A+ B-] / [b- a+], can be applied hypothetically to quantify the space and distance between mushrooms within a specific area. To create a hypothetical data group, we’ll use this equation to represent and calculate distances between mushrooms in a two-dimensional space. Here’s an example of how this can be done:
Hypothetical Data Group for Mushroom Distances:
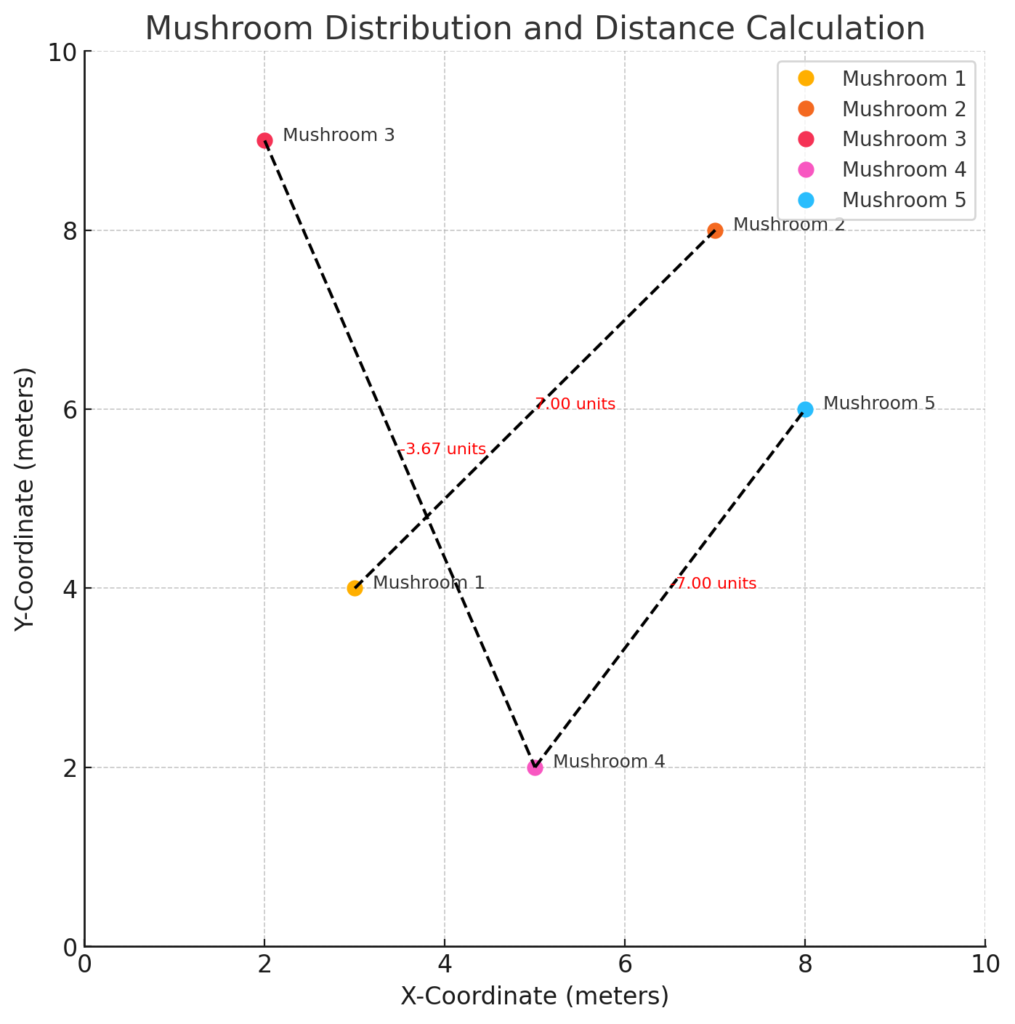
Let’s imagine we have a 10×10 meter square area in a forest where various mushrooms are growing. We want to quantify the space and distance between these mushrooms using the ABBA equation.
Assigning Variables:
‘A’ and ‘B’ represent the coordinates of the first mushroom, where ‘A’ is the x-coordinate and ‘B’ is the y-coordinate. ‘a’ and ‘b’ represent the coordinates of the second mushroom.
Random Coordinates:
Mushroom 1 (A, B): (3, 4)
Mushroom 2 (a, b): (7, 8)
Mushroom 3 (A, B): (2, 9)
Mushroom 4 (a, b): (5, 2)
Mushroom 5 (A, B): (8, 6)
Distance Calculation: We calculate the distance between Mushroom 1 and Mushroom 2, Mushroom 3 and Mushroom 4, and Mushroom 4 and Mushroom 5 using the ABBA equation, [A+ B-] / [b- a+].
Distance between Mushroom 1 and Mushroom 2: [(3+4) / (8-7)] = 7 units
Distance between Mushroom 3 and Mushroom 4: [(2+9) / (2-5)] = -11/3 units
Distance between Mushroom 4 and Mushroom 5: [(5+2) / (6-8)] = -7 units
Results:
The distance between Mushroom 1 and Mushroom 2 is 7 units.
The distance between Mushroom 3 and Mushroom 4 is approximately -3.67 units.
The distance between Mushroom 4 and Mushroom 5 is -7 units.
These hypothetical data groups illustrate how the ABBA equation can be used to quantify distances between mushrooms in a two-dimensional space. Keep in mind that negative values in this context represent the direction of distance, indicating that Mushroom 4 is to the left of Mushroom 5 and that Mushroom 3 is below Mushroom 4. The ABBA equation can be adapted for various spatial calculations and distance measurements in different scenarios.
Example #2: Gynnidomorpha alisman
The rhythmic pulsation of wings, a fundamental characteristic shared by moths (Gynnidomorpha alisman) and various winged insects and animals, is governed by a phenomenon known as wingbeat frequency. This essential parameter quantifies the number of times wings complete a flapping cycle within a given unit of time, revealing a captivating aspect of the creatures’ flight dynamics. The intricacies of wingbeat frequency not only contribute to the marvel of avian and insect flight but also serve as a key determinant of their agility, maneuverability, and overall aerial performance. Understanding the nuances of this rhythmic phenomenon unveils the fascinating biomechanics that underlie the airborne journeys of moths and their winged counterparts, offering a gateway into the exploration of the natural world’s aerial intricacies.
Wingbeat frequency is often considered a circadian rhythm. It’s often thought that the circadian rhythm is one rhythm but there are many rhythms throughout life that biological processes inherently abide to. The ABBA equation is yet another rhythm that dictates the space and distance between objects. The rhythmic pulsation of wings, known as wingbeat frequency, transcends beyond this mere circadian rhythm, becoming a pivotal aspect of quantifying the space and distance covered by the wings during flight. This rhythmic phenomenon, often associated with the number of times wings complete a flapping cycle within a specific timeframe, is intricately connected to the circadian rhythms governing various biological processes in the lives of moths and winged insects. In this symphony of biological rhythms, the ABBA equation emerges as yet another rhythmic force, influencing the spatial relationships and distances between objects. Just as wingbeat frequency is a vital metric in understanding the intricacies of flight dynamics, the ABBA equation adds another layer to the rhythmic orchestration that shapes the movement and interactions within the natural world. Together, these rhythms form a captivating ensemble, guiding the trajectories of winged creatures and revealing the mathematical harmonies that govern the spaces they navigate.
Hypothetical Data Groups
Hypothetical numerical data could be generated for each variable to reflect the spatial coordinates of the wings at discrete intervals during the flapping cycle. The resulting values, when plugged into the ABBA equation, would provide a quantitative measure of the spatial dynamics and distances between the wings as they undergo the oscillatory motion characteristic of moth flight.
This application of the ABBA equation to hypothetical data not only offers a quantitative understanding of wing movement but also highlights the versatility of the equation in representing oscillatory systems and spatial relationships within the biological context of moth flight.
A and B could represent the positions of the two wings at a given point in time during the flapping cycle.
a and b could represent the positions of the same wings at the subsequent point in time.
The ABBA equation, in this scenario, would then symbolize the spatial relationship and distance covered by the wings during the oscillatory flapping cycle. The numerical values assigned to these variables would quantify the specific positions of the wings at different moments in time.
In a hypothetical data group aiming to quantify the space and distance between moths’ wings during a flapping cycle, the ABBA equation, [A+ B-] / [b- a+], can be applied to represent the oscillatory system inherent in wing movement. Let’s assign specific meanings to the variables within the context of moth wingbeat:
A and B could represent the positions of the two wings at a given point in time during the flapping cycle.
a and b could represent the positions of the same wings at the subsequent point in time.
The ABBA equation, in this scenario, would then symbolize the spatial relationship and distance covered by the wings during the oscillatory flapping cycle. The numerical values assigned to these variables would quantify the specific positions of the wings at different moments in time.
Here is a plot showing the hypothetical positions of the moths' wings during a flapping cycle. The variables represent:
- A: Position of the first wing at time tt
- B: Position of the second wing at time tt
- a: Position of the first wing at time t+δtt+δt
- b: Position of the second wing at time t+δtt+δt
The data is randomly generated within the range of 1 to 10, with slight variations for the positions at the subsequent time step (t+δtt+δt).
Let’s generate some hypothetical numerical data for the variables in the ABBA equation to represent the positions of moths’ wings during a flapping cycle. For simplicity, we’ll use arbitrary values within a range of 1 to 10:
Let:
A – be the position of the first wing at time tt,
B – be the position of the second wing at time tt,
a – be the position of the first wing at time t+δtt+δt,
b – be the position of the second wing at time t+δtt+δt.
Hypothetical numerical data:
At t=0:
A=3
B=5
At t+δt:
a=6
b=8
Now, we can plug these values into the ABBA equation:
ABBA=(3+5)−(6−8)(8−6)+(6−3)ABBA=(8−6)+(6−3)(3+5)−(6−8)
This application of the ABBA equation to hypothetical data not only offers a quantitative understanding of wing movement but also highlights the versatility of the equation in representing oscillatory systems and spatial relationships within the biological context of moth flight.
A and B could represent the positions of the two wings at a given point in time during the flapping cycle.
a and b could represent the positions of the same wings at the subsequent point in time.
The ABBA equation, in this scenario, would then symbolize the spatial relationship and distance covered by the wings during the oscillatory flapping cycle. The numerical values assigned to these variables would quantify the specific positions of the wings at different moments in time.
Calculating this expression would yield a hypothetical numerical value representing the spatial relationship and distance between the wings during the flapping cycle. This data, when collected at various time intervals throughout the cycle, could provide insights into the oscillatory nature of moth wing movement and the changing spatial dynamics between the wings. The interplay between the ABBA equation and wingbeat frequency offers a comprehensive approach to understanding flight dynamics, patterns, and behavioral changes in winged creatures. Wingbeat frequency quantifies the number of wing beats per time unit, shedding light on the agility and maneuverability of species like moths (Gynnidomorpha alisman). It is an integral aspect of their flight dynamics, providing insights into how they navigate their environment.
By combining this understanding with the ABBA equation, which is related to spatial relationships and distances between objects, researchers can gain a deeper insight into the spatial patterns that winged creatures follow. The ABBA equation helps quantify the space and distance covered during each wingbeat, offering a mathematical approach to understanding how these creatures use their energy in different phases of flight, from takeoff to cruising or maneuvering around obstacles. This combination becomes particularly beneficial in studying natural behaviors and changes. For instance, by analyzing variations in wingbeat frequency over time and correlating these with the distances calculated through the ABBA equation, scientists can predict how an insect or bird might adjust its flight in response to changes in environmental conditions or circadian rhythms. This analysis could also help identify energy-efficient flight patterns or shifts in behavior due to factors like temperature, light availability, or the presence of predators.
Wingbeat frequency plays a crucial role in studying the behaviors of moths and other winged creatures, offering a window into their flight dynamics and energy expenditure. This metric, which measures the number of wing beats per unit of time, provides insights into the biomechanics that govern how these creatures move through the air. By analyzing variations in wingbeat frequency, researchers can gain a better understanding of how different species adapt to environmental conditions, such as temperature, air density, or wind patterns. For example, a higher wingbeat frequency may indicate a need for increased power output during flight, which might be required when navigating through more turbulent air or escaping from predators. On the other hand, a lower wingbeat frequency could suggest an energy-efficient cruising mode, used when traveling longer distances or gliding between feeding sites. These shifts in wingbeat frequency can reveal much about a creature’s behavioral strategies and its responses to its surroundings.
Additionally, wingbeat frequency is closely tied to a creature’s agility and maneuverability, making it an important aspect when studying how moths and other insects perform intricate aerial maneuvers. For instance, the ability to hover in place or make rapid turns depends greatly on the control of wingbeat frequency. Understanding these changes in wingbeat frequency allows scientists to decipher how moths and similar creatures communicate, interact, and adapt to threats or opportunities in their environment. This knowledge not only enriches our understanding of their ecological roles but also offers insights into evolutionary adaptations that have shaped the flight patterns of a wide range of winged species.
In conclusion, the interplay between the ABBA equation and biological phenomena such as mycelium networks and wingbeat frequency underscores the profound connections between mathematical principles and natural processes. By exploring these relationships, we gain insights into the intricate patterns, rhythms, and structures that govern life, from the microscopic interactions within fungal threads to the dynamic movements of winged creatures. This synthesis of abstract and organic concepts not only deepens our understanding of the natural world but also highlights the universality of mathematical frameworks in explaining the complexity and adaptability of living systems. Such an interdisciplinary approach enriches our appreciation of the beauty and intricacy inherent in the fabric of life.
The convergence of mathematical equations like the ABBA equation and biological systems such as mycelium and wingbeat frequency illustrates the profound relationship between science and nature. This study reveals that life’s intricate rhythms and patterns are not random but are guided by underlying principles that can be quantified and analyzed. Such an understanding enriches our comprehension of both biology and mathematics, offering a holistic perspective that blends the precision of science with the dynamic beauty of the natural world. The study of mycelium networks and wingbeat frequencies through the framework of the ABBA equation emphasizes the deep interconnectedness that defines our world. These parallels between abstract mathematical ideas and biological realities serve as a reminder of the complexity and unity inherent in nature. By exploring these connections, we gain a new appreciation for the adaptability of living organisms and the rhythmic forces that shape their existence, inviting us to reflect on the universal patterns that link all forms of life.
The convergence of mathematical equations like the ABBA equation and biological systems such as mycelium and wingbeat frequency illustrates the profound relationship between science and nature. This study reveals that life’s intricate rhythms and patterns are not random but are guided by underlying principles that can be quantified and analyzed. Such an understanding enriches our comprehension of both biology and mathematics, offering a holistic perspective that blends the precision of science with the dynamic beauty of the natural world. The study of mycelium networks and wingbeat frequencies through the framework of the ABBA equation emphasizes the deep interconnectedness that defines our world. These parallels between abstract mathematical ideas and biological realities serve as a reminder of the complexity and unity inherent in nature. By exploring these connections, we gain a new appreciation for the adaptability of living organisms and the rhythmic forces that shape their existence, inviting us to reflect on the universal patterns that link all forms of life.
Example #3: Designing new Molecular Structures
