ABBA Equation
Summary
This page discusses the ABBA equation, represented as [A+ B-] / [b- a+], which was initially retrieved from a meditation through the author, and explores its various interpretations and applications. It begins by highlighting the equation’s potential connection to the concept of calculating space or distances between objects, emphasizing its symbolic and abstract nature. Then dives into multiple examples and scenarios in which the equation can be applied, ranging from chemical diffusion to population dynamics. It also explores the significance of graphing the equation, demonstrating how it can provide valuable insights and facilitate quantitative analysis. Furthermore, it draws a unique and intriguing connection between the ABBA equation and the art of weaving, showcasing the rhythmic and repetitive nature of both the equation and the craft. In this context, ‘A’ and ‘B’ symbolize warp and weft threads, while ‘+’ and ‘-‘ represent the actions of lifting and lowering threads on a loom, demonstrating how mathematics can find resonance in creative human endeavors. In conclusion, the ABBA equation represents an abstract mathematical expression that can be correlated with various concepts, including measuring space between objects, and it exemplifies the versatility of mathematical thinking. However, its practical application as a tool for measurement necessitates the assignment of specific numerical values to its variables. Then provides a comprehensive exploration of the ABBA equation’s diverse interpretations and applications, shedding light on its potential significance in various fields.
Introduction
The Belousov-Zhabotinsky reaction (BZ reaction) is an example of a nonlinear chemical oscillator, in which bromine and an acid are involved. It is a far from equilibrium reaction that remains so for a significant length of time and evolves chaotically. The BZ reaction is a chemical oscillatory reaction that fluctuates in color, which resembles a mathematical proof of the universe as a matrix. This particular proof shows that the universe operates in a matrix form and that subjective experience and objective manifestation are constantly oscillating, which the BZ reaction visually represents. The visual representation of the BZ reaction provides insight into the relationship between math and physics. The mathematical representation [A+ B-] / [b- a+] is related to the BZ reaction, as both are oscillating systems. The square brackets in the equation indicate a matrix, which is a way of representing linear transformations in mathematics. The BZ reaction visually represents this concept by producing two expanding spirals, which can be seen as a physical representation of subjective experience and objective manifestation oscillating and constantly manifesting.
The BZ reaction produces expanding spirals, which in the LSF framework are seen as expressions of light. This visual representation has been linked to the mathematical concept of PI, which is seen as explaining the linear and nonlinear characteristics of subjective experience and objective manifestation. In this perspective, the physical world is constantly oscillating between the two, and the BZ reaction provides a physical visual representation of this idea. The BZ reaction is a chemical oscillatory reaction that serves as an example of non-equilibrium thermodynamics. The concept of the BZ reaction has been linked to the mathematical concept of PI, which explains the linear and nonlinear characteristics of subjective experience and objective manifestation.
ABBA & Cellular Automaton
The ABBA equation, represented as [A+B−]/[b−a+], provides an intriguing lens for analyzing how interactions between different entities can influence spatial arrangements. At its core, this equation seems to represent a ratio of positive and negative states or influences. The term [A+B−] could symbolize a combination of positive states associated with entity A and negative states from entity B, while the denominator [b−a+] could represent negative states linked to entity b and positive states of entity a. In the context of spatial analysis, such an equation could be interpreted as a way to model how certain forces or states balance each other out across a given space. For example, it could describe how attractive and repulsive forces between objects (such as gravitational or magnetic attractions) interact to influence their distribution within a space. The numerator might reflect the strength of attractive forces that draw objects closer together, while the denominator could represent repulsive forces that push them apart, thereby determining how they position themselves relative to one another. This balance of interactions is crucial for understanding the dynamics of spatial distribution in various physical systems, from the arrangement of celestial bodies in space to the organization of molecules in a solution.
Cellular automata (CA), on the other hand, offer a computational approach to understanding spatial relationships by modeling complex systems through simple rules. A cellular automaton consists of a grid of cells, where each cell evolves over time based on a set of rules that consider the states of neighboring cells. Despite their simplicity, cellular automata are capable of simulating intricate patterns and behaviors that emerge from local interactions. In the context of understanding the spaces between objects, cellular automata are particularly valuable because they can demonstrate how these objects organize themselves through the iterative application of rules. For instance, they can simulate how particles might cluster together, how gaps or voids appear between them, and how these patterns evolve as the system progresses. This approach is especially powerful in revealing emergent properties—behaviors or patterns that arise from the collective interaction of many simple elements, which are not easily predicted by analyzing individual interactions alone. Cellular automata thus serve as a kind of digital laboratory for exploring how local interactions can lead to complex global arrangements, providing insights into the dynamic nature of spaces between objects.
When considering the interplay between concepts like the ABBA equation and cellular automata, their combined use becomes significant for analyzing and calculating the spaces between objects in dynamic systems. The ABBA equation allows for a theoretical understanding of how different forces balance each other, offering a way to predict the distances or spatial configurations that result from these interactions. This is particularly relevant in systems where multiple entities exert varying levels of attraction and repulsion, such as particles in a fluid or even social interactions within a population. Cellular automata, meanwhile, provide a practical method for visualizing how such systems might evolve over time. By simulating the rules that govern the behavior of individual components, they reveal how the overall pattern of spacing between objects emerges and changes, offering a detailed view of the dynamic processes that shape spatial arrangements.
Together, the ABBA equation and cellular automata offer complementary perspectives that are valuable for both theoretical and practical analyses of spatial systems. They provide a framework for understanding how local interactions between objects—whether driven by physical forces, chemical reactions, or even social dynamics—translate into larger patterns of organization. This combination can be applied in diverse fields, from optimizing the arrangement of urban structures in city planning to understanding molecular interactions in chemistry or modeling ecological distributions in natural environments. By exploring how spaces are formed, modified, and maintained between objects, these concepts allow for a deeper appreciation of the underlying principles that shape the physical and abstract structures of our world.
The ABBA equation can be considered an example of cellular automata, particularly if it is formulated as a set of rules governing the behavior of cells in a grid-like structure. Cellular automata are mathematical models used to simulate complex systems in which individual cells or entities interact with their neighbors according to predefined rules, and the ABBA equation can be conceptualized in this framework.
Here’s how you can view the ABBA equation as a cellular automaton:
1. Grid Structure:
In a cellular automaton, you have a grid of cells, and each cell can be in one of several states. In the context of the ABBA equation, you can think of the grid as representing the spatial domain in which chemical reactions occur.
2. Cell States:
The ABBA equation would assign different states or values to each cell based on the concentrations of the chemical species A and B. These concentrations can change over time due to chemical reactions, which are described by the equation.
3. Neighborhood Interaction:
Cellular automata operate based on local interactions, where each cell’s state is determined by the states of its neighboring cells. Similarly, in the ABBA equation, the concentrations of A and B at a particular location can be influenced by the concentrations of A and B in adjacent locations due to diffusion or reaction processes.
4. Update Rules:
In cellular automata, there are specific rules that dictate how a cell’s state changes over time. In the ABBA equation, the chemical reactions and diffusion processes are described by mathematical equations, which serve as the rules governing how the concentrations of A and B change over time. These equations can be seen as the update rules for the chemical system.
5. Time Steps:
Cellular automata progress in discrete time steps, where the state of each cell is updated based on the state of its neighbors and the predefined rules. Similarly, in the ABBA equation, time would progress in discrete steps, with the concentrations of A and B evolving based on the chemical reactions and diffusion processes at each time step.
In essence, the ABBA equation can be seen as a mathematical representation of a cellular automaton, with the grid representing the spatial domain, the cell states representing the concentrations of chemical species, and the equation itself defining the rules that govern how these concentrations change over time. This view allows us to analyze the chemical dynamics of the system in a manner similar to how cellular automata are used to study complex systems and pattern formation.
Examples
The ABBA equation, denoted as [A+ B-] / [b- a+], opens a door to intriguing exploration across various domains. While unconventional in mathematical terms, this equation serves as a gateway to understanding complex relationships. It prompts a dive into the intricacies of its variables, such as ‘A,’ ‘B,’ ‘a,’ and ‘b,’ and the actions represented by ‘+’ and ‘-‘, revealing a world of meaningful results. Whether examined from a theoretical or practical perspective, the ABBA equation showcases the power of mathematical reasoning in tackling complex phenomena and yielding enlightening solutions. This symbolical equation, abstract in its essence, can also find resonance in the realm of spatial calculation, hinting at its potential to measure distances between objects. Yet, it’s essential to underscore that this symbolism becomes tangible and operational only when specific numerical values and units are assigned to the equation’s variables. This equation, in its abstract and symbolic form, paves the way for a myriad of explorations and applications.
Example 1: Chemical Diffusion
Imagine a 2D grid where each cell represents a tiny region in a petri dish containing a chemical solution. In this case, the ABBA equation could describe the diffusion of two chemicals, A and B. The concentration of A and B in each cell would evolve over discrete time steps based on their diffusion rates and reactions with each other and the neighboring cells. The ABBA equation, in this context, would be the set of rules governing how the concentrations of A and B change over time due to diffusion and chemical reactions, making it akin to a cellular automaton modeling the spreading of chemicals.
Example 2: Reaction-Diffusion System
Imagine a grid representing a chemical reaction-diffusion system on a 2D surface. The grid’s cells represent locations on the surface, and the values within the cells represent the concentrations of two reacting substances, A and B. The ABBA equation defines the rules for how these concentrations change over time due to chemical reactions (e.g., A reacting with B) and the diffusion of these substances to neighboring cells. In this scenario, the ABBA equation resembles a cellular automaton, with each cell’s state evolving based on the states of its neighboring cells and predefined reaction-diffusion rules.
Example 3: Population Dynamics
These hypothetical examples demonstrate how the ABBA equation, when applied to various systems, can be seen as a cellular automaton by modeling the spatial and temporal evolution of entities or concentrations based on predefined rules and interactions with neighboring entities or concentrations. The underlying principles of cellular automata apply to a wide range of systems beyond traditional grid-based simulations, and the ABBA equation can serve as a mathematical representation of such systems.
Solving the ABBA Equation
Solving the ABBA equation, represented as [A+ B-] / [b- a+], presents an intriguing mathematical challenge that calls for a thorough understanding of its components and operations. While this equation may not be a standard mathematical formula, its unique structure offers a distinctive opportunity to explore the interplay between variables and mathematical operations. In this exploration, we dive into the intricate process of solving the ABBA equation, shedding light on how the values of ‘A,’ ‘B,’ ‘a,’ and ‘b’ and the actions denoted by ‘+’ and ‘-‘ can combine to yield meaningful results.
Solving the ABBA Equation: [A+ B-] / [b- a+]
The equation, [A+ B-] / [b- a+], contains variables and symbols enclosed in square brackets. To visually solve it, you would typically follow standard mathematical operations, but let's break it down step by step:
1. Identify the variables:
A and B are variables with positive exponents.
a and b are variables with negative exponents.
2. Recognize that [A+ B-] represents the numerator, while [b- a+] represents the denominator.
3. Perform the mathematical operations:
In the numerator, [A+ B-], you’re adding A and subtracting B.
In the denominator, [b- a+], you’re subtracting a and adding b.
4. Write the equation without the square brackets for clarity: (A + B) / (b – a)
So, visually solving the equation, you’ve simplified it to (A + B) / (b – a). This is the final form of the equation after performing the operations.
Examples for Solving the ABBA Equation: [A+ B-] / [b- a+]
The equation (A + B) / (b – a) is a general mathematical expression that can represent a wide range of mathematical problems. To provide specific solutions, you would need to have values for the variables A, B, a, and b or more context about the problem being addressed.
Example 1: If A = 5, B = 3, a = 2, and b = 1, then the solution would be: (5 + 3) / (1 – 2) = 8 / (-1) = -8
Example 2: If A = 10, B = 2, a = 3, and b = 7, then the solution would be: (10 + 2) / (7 – 3) = 12 / 4 = 3
You can substitute different values for A, B, a, and b to find various solutions to the equation. The actual solution will depend on the specific values of the variables provided.
In conclusion, the equation (A + B) / (b – a) is a mathematical expression that represents a ratio between the sum of variables A and B in the numerator and the difference between variables b and a in the denominator. The solution to this equation will vary based on the specific values assigned to A, B, a, and b. To find a solution, you would need to provide numerical values for these variables or a context-specific problem that can be addressed using this equation. Without such values or context, it remains a general mathematical expression that can take on different values and meanings depending on the specific inputs.
Graphing the Equation
The graph of the equation [A+ B-] / [b- a+] is highly dependent on the specific numerical values assigned to the variables ‘A,’ ‘B,’ ‘a,’ and ‘b.’ The appearance of the graph can exhibit diverse characteristics, such as linear relationships, asymptotes, discontinuities, and various curves or patterns. In scenarios where ‘A’ and ‘B’ remain constant and ‘a’ and ‘b’ vary linearly, the graph might manifest as a straight line, with its slope and intercept determined by ‘A’ and ‘B.’ The presence of asymptotes or discontinuities can occur when ‘a’ and ‘b’ values lead to division by zero or undefined expressions. More complex relationships between the variables can result in a multitude of shapes and patterns. Therefore, the visual representation of this equation through graphing software or tools will offer insights into its behavior based on the specific values used, revealing the diverse mathematical relationships it may exhibit. Translating the equation [A+ B-] / [b- a+] into a graph where the variables are represented as ‘X’ and ‘Y’ transforms the abstract mathematical expression into a tangible visual representation. To achieve this, you select a relevant range of values for ‘X’ and ‘Y’ and systematically calculate ‘Y’ for each ‘X’ value using the equation, where ‘X’ corresponds to ‘A’ and ‘Y’ to ‘B.’ ‘a’ and ‘b’ may be constants or specified values. The resultant data points, each representing a specific ‘X’ and ‘Y’ pair, are then plotted and connected to form a curve or line on the graph. This graph, in turn, offers a comprehensive insight into the intricate relationship between ‘X’ and ‘Y.’ It allows for the identification of patterns, trends, and other key characteristics, thereby enhancing the understanding of how ‘X’ influences ‘Y’ quantitatively, making it a valuable tool for scientific analysis, modeling, and prediction across a spectrum of fields.
The Significance of Zero
In the context of a graph representing the ABBA equation, where ‘zero’ is encountered, it signifies an important aspect related to the space between objects. When the value on the graph reaches zero, it indicates that there is no space, or the space between the objects has effectively collapsed or disappeared. This can have real-world implications. For example, if ‘A’ and ‘B’ represent objects, and ‘a’ and ‘b’ represent their positions, then when the graph of [A+ B-] / [b- a+] approaches zero, it suggests that the objects ‘A’ and ‘B’ have moved so close to each other that the space between them is negligible or even non-existent. This can be relevant in scenarios involving particles, celestial bodies, or any other objects where the concept of minimal or zero space between them is meaningful. In summary, zero on the graph indicates that the space between objects has diminished to the point where they are essentially in direct contact or are extremely close to each other.
Hypothetical Data Group
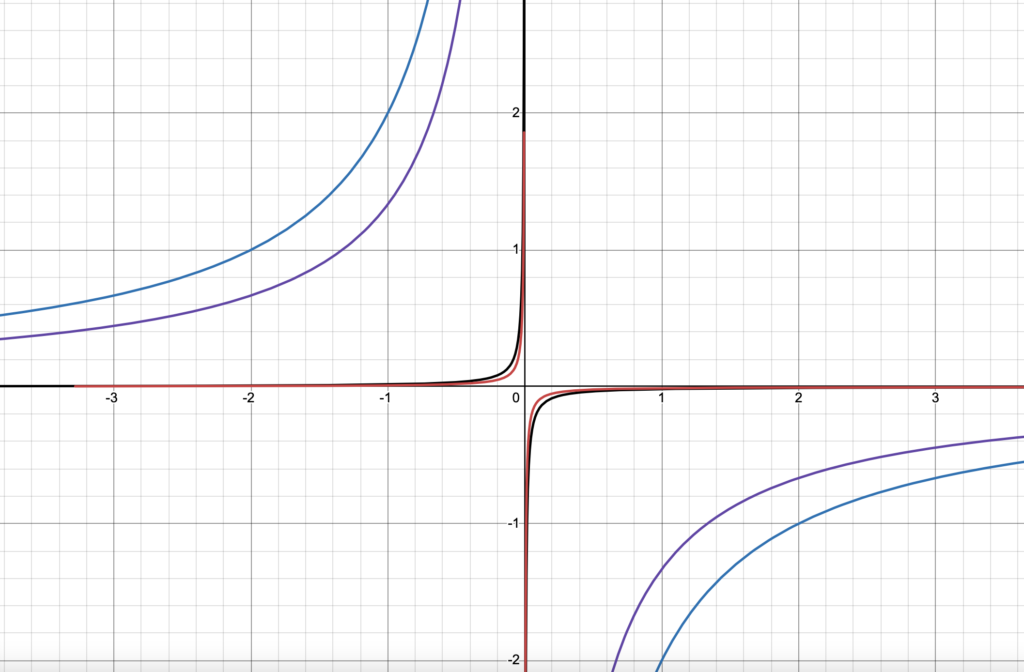
Blue line: Planet B Distance
Purple line: Planet A Distance
Red line: Size of Planet A
Black line: Size of Planet B