Using ABBA to Compute Inertia

Introduction
The ABBA equation, expressed as [A+B−]/[b−a+], offers a unique framework for understanding interactions between opposing forces in various scientific fields, including AstroScience and physics. Its abstract structure, which balances different states of attraction and repulsion, makes it particularly useful for modeling the dynamics of celestial bodies, where gravitational pull and cosmic expansion play crucial roles. By applying the ABBA equation to hypothetical data, we gain insights into how these forces interact, providing a fresh perspective on the relationship between inertia, motion, and cosmic distances. This analysis explores the application of the ABBA equation to understand the equilibrium states in the cosmos, offering a deeper understanding of the natural balance that sustains celestial systems.
To compute inertial measurements and analyze the ABBA equation in this context, let’s break down the ABBA equation and see how it can conceptually apply to physical principles like inertia and interactions in AstroScience. The ABBA equation is given by:
[A+B−]/[b−a+]
Interpretation of Terms
- A+ and B-: These might represent opposing or complementary forces or states. For example, in a cosmic context, A+ could be a force of attraction (like gravity), while B- could be a force of repulsion or separation (like a magnetic field or cosmic expansion).
- b- and a+: These could represent opposing phases or energy states that counterbalance A+ and B-.
Applying the Equation to Inertial Measurements
Inertia is fundamentally about an object’s resistance to changes in its state of motion. This ties closely with concepts of equilibrium and dynamic balance, which are central to the interpretation of the ABBA equation.
1. Inertia and Cycles
- Inertia maintains a body’s state of motion unless acted upon by external forces. The structure of the ABBA equation could represent this concept with A+ and B- symbolizing different states or forces that maintain an object’s inertia.
- A+ could symbolize a force that initiates motion (like an impulse), while B- could represent a force that counteracts or dampens it (like friction or air resistance).
- The terms b- and a+ could represent forces that sustain motion or states that restore balance when a body deviates from equilibrium.
2. AstroScience Applications
- In a cosmic setting, let’s assume A+ represents a gravitational pull between two celestial bodies, while **B-**represents a separating force (like cosmic expansion or centrifugal force due to rotation).
- The denominator, b- a+, could represent adjustments or counterbalancing forces, like the inertia of the bodies themselves or their resistance to changes in relative positioning.
- In this case, the ABBA equation could describe how the relationship between gravitational attraction and repulsion due to cosmic expansion determines the relative positions and distances between celestial bodies over time.
Computation Example
To demonstrate the concept with a simplified example, let’s consider how this equation might help determine a stable distance between two celestial objects under the influence of attraction and repulsion.
A+ = Gravitational force (Fg=Gr2m1m2)
Let:
Fg=Gm1m2r2
B- = Expanding force (Fe=k⋅r, where k is a constant related to cosmic expansion)
Fe=k⋅r
k
b- = Inertial resistance (m2v2/r) of one body due to its velocity
m2v2/r
a+ = Additional counteracting force like radiation pressure (L/(4πr2c))
L/(4πr2c)
The ABBA equation would then relate these forces as:
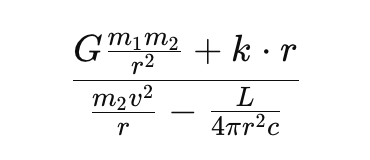
This equation could describe a stable radius (rr) at which the forces balance, giving insight into the spatial relationships between the two objects. It can also help evaluate how changes in one force (e.g., a change in kk, representing expansion) would affect the balance of the system.
This symbolic interpretation of the ABBA equation allows it to be applied to various physical scenarios, highlighting the balance of forces that maintain equilibrium, be it in a cosmic system or an object in motion due to inertia.
Hypothetical Celestial Interaction Data
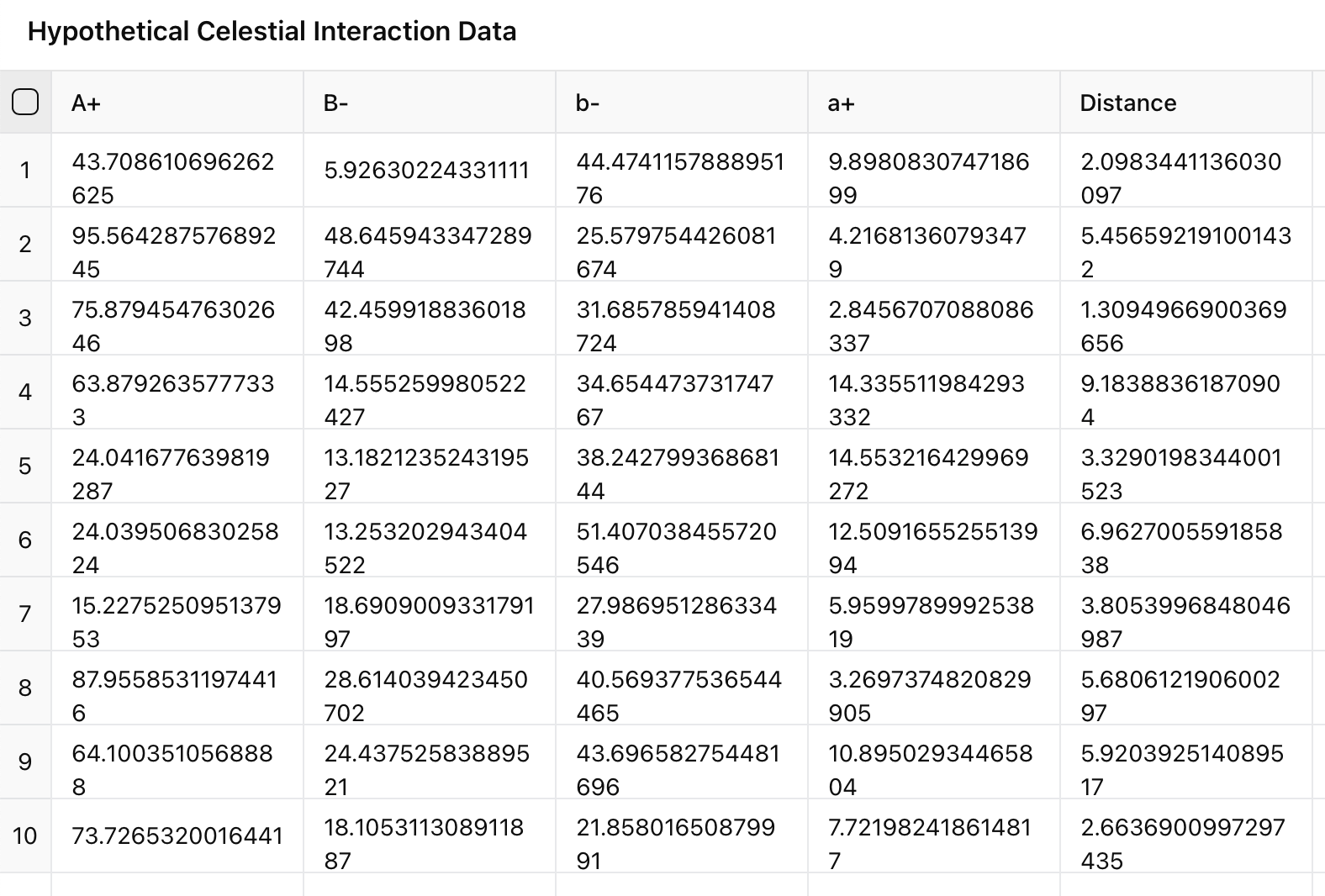
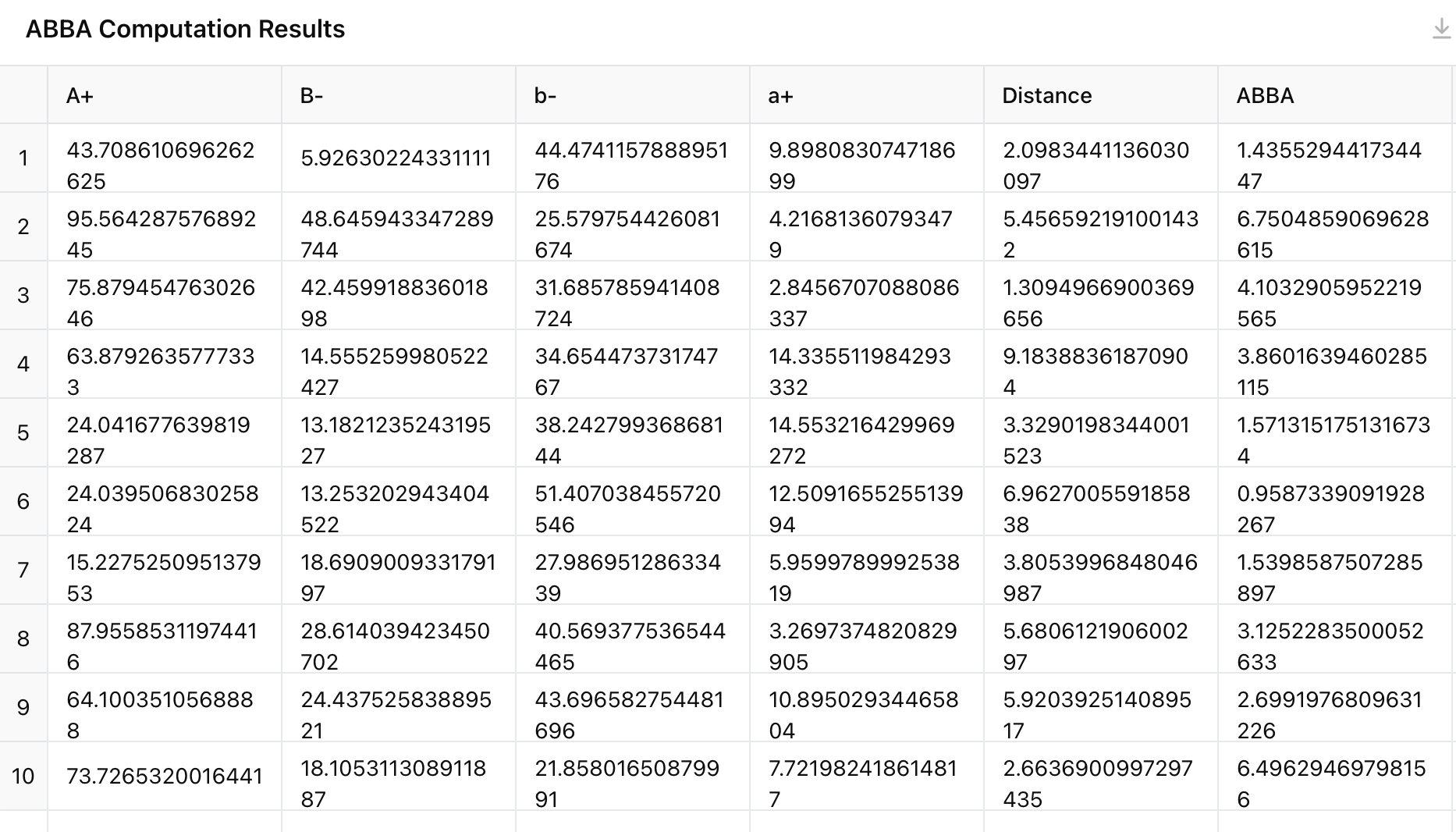
The ABBA values for the hypothetical dataset have been computed using the formula
(A++B−)/(b−−a+)
(A++B−)/(b−−a+). This result represents the balance between the gravitational and expanding forces relative to the counterbalancing effects. You can explore how these values change in relation to the forces and distance between the celestial bodies.
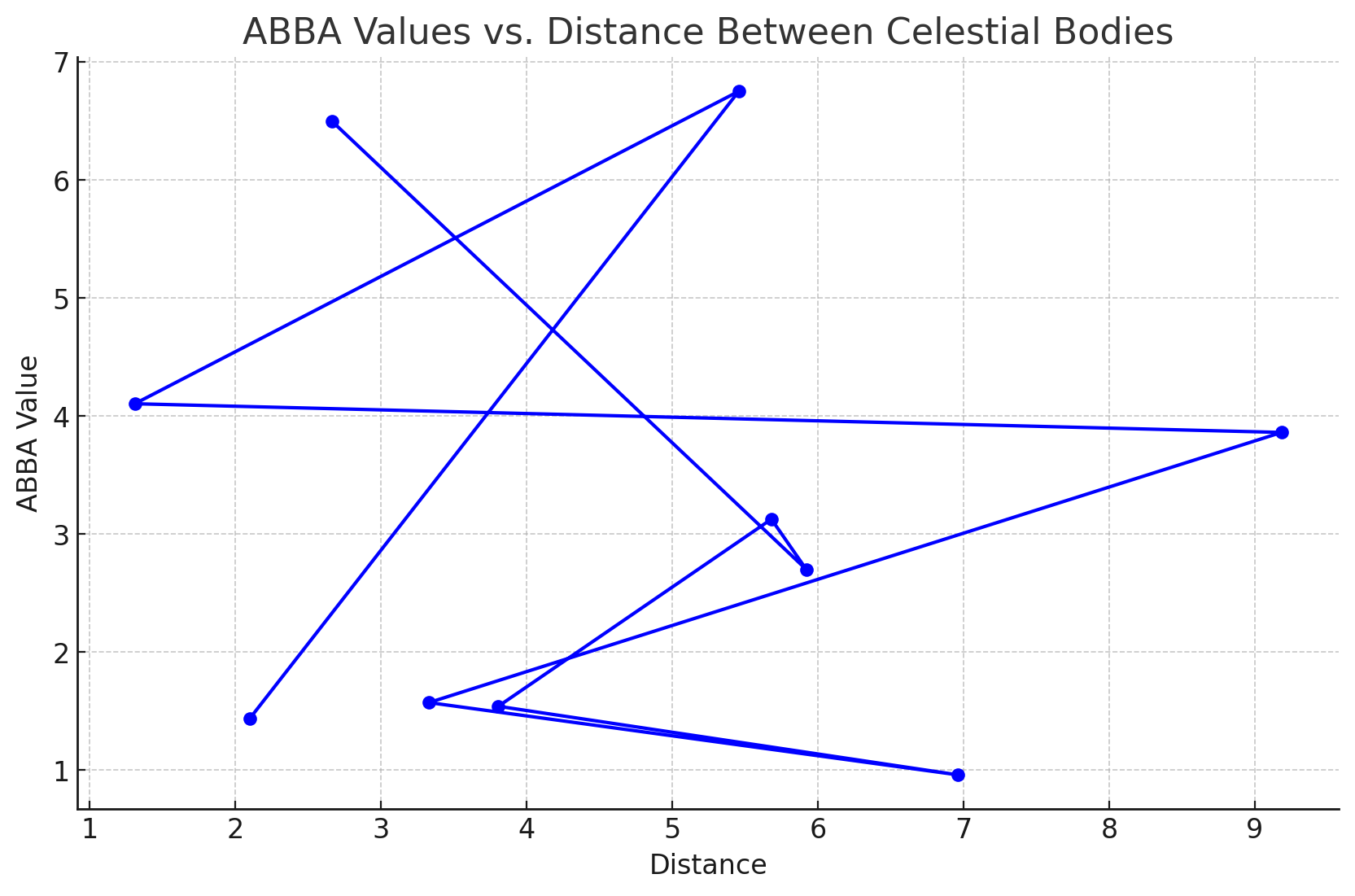
Here is the plot showing the relationship between the ABBA values and the distance between celestial bodies. This visualization helps to understand how the balance of forces (gravitational, expanding, inertial, and counteracting) varies as the distance between these bodies changes.
Conclusion
The ABBA equation serves as a powerful tool for interpreting the interplay of forces in astrophysical contexts. Through the computation and visualization of ABBA values, we can see how the balance between gravitational attraction, cosmic expansion, inertial resistance, and counteracting forces shapes the distances between celestial bodies. This approach allows for a deeper appreciation of how dynamic equilibrium is maintained in the universe. By modeling these interactions, the ABBA framework helps to bridge abstract mathematical concepts with real-world phenomena, providing a versatile perspective that can extend beyond the realm of astrophysics to other areas where opposing forces shape outcomes.