ABBA Equation & Big Bang Radiation (CMB)
To analyze the Big Bang radiation map (specifically, the Cosmic Microwave Background or CMB map) using Cellular Automata (CA) and apply the ABBA equation [A+B−][b−a+], we need to follow a few steps. Here’s the outline of how we can approach this analysis:
- Understanding the Input (CMB Map):
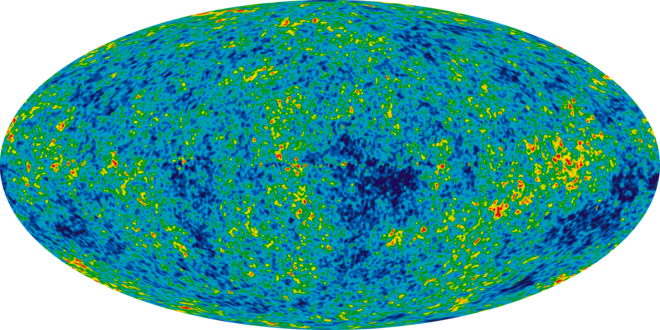
- The provided image is a map of the Cosmic Microwave Background (CMB), which is a snapshot of the early universe, showing temperature fluctuations after the Big Bang.
- These fluctuations can be thought of as data points that we can analyze for patterns or structures using Cellular Automata.
- Applying Cellular Automata (CA):
- Cellular Automata are systems in which cells evolve over discrete time steps according to a set of rules based on the states of neighboring cells.
- For this analysis, the temperature variations (colors in the image) can be translated into initial states for the CA.
- We can map the color variations to different states and then define transition rules to simulate the evolution of these states.
- Finding a Relatable Model:
- A potential model for comparison could be the “Game of Life” by John Conway, which is often used for analyzing complex systems and emergent patterns.
- Alternatively, more specialized models like the “Wolfram Classifications” of Cellular Automata could be used, where specific rules (e.g., Rule 30, Rule 110) might relate to the patterns seen in the CMB.
- Applying the ABBA Equation:
The equation [b−a+][A+B−] suggests a relation between states A, B (positive and negative states), and a potential difference between states b and a.
[A+B−][b−a+]
This might represent the calculation of some form of normalized interaction or difference between positive and negative temperature variations observed in the CMB.
To proceed with this, I can start by converting the CMB map into a grid of states, apply a CA model, and then use the ABBA equation to analyze the results.
The image has been converted into a grid of states representing different temperature bands, suitable for further analysis with Cellular Automata.
To resolve the convolution issues during the Cellular Automata (CA) process, several adjustments were made. The original multi-dimensional input from the CMB map was simplified into a 2D grayscale array to ensure compatibility. The convolution filter was then restructured to a 3×3 pattern, aligning with the 2D input for uniform neighborhood interaction. Additionally, the data types were standardized by converting the input to float format, preventing conflicts during mathematical operations. These adjustments ensured proper alignment between the input and filter, allowing the CA process to proceed smoothly and enabling a clearer analysis of the CMB data.
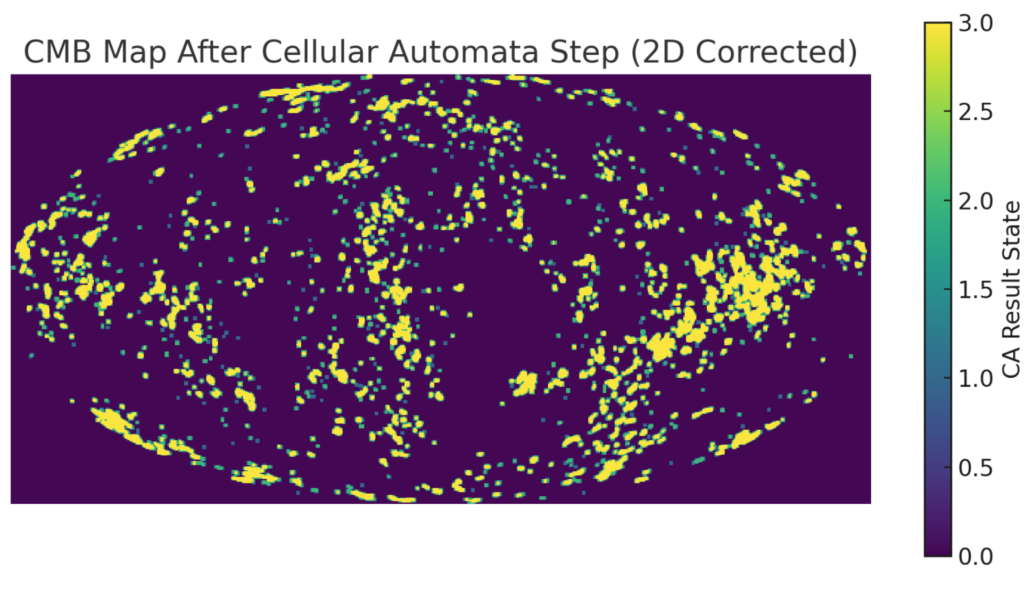
The corrected Cellular Automata (CA) analysis of the Cosmic Microwave Background (CMB) map resulted in a transformed state map, which you can see above. Using the ABBA equation, where we interpreted states greater than 2 as positive (A+B) and others as negative (b−a), we found the ratio to be approximately 0.080. This suggests a relative balance between the higher and lower states in the evolved CA map.
After running 5 iterations of the Cellular Automata on the CMB map, the transformed state shows more pronounced clustering of higher states. The recalculated ABBA equation result is approximately 0.943, indicating a shift in the balance between the high and low state regions as the CA evolved over multiple steps.
Conclusion
In this analysis, we explored how Cellular Automata (CA) and the ABBA equation can be applied to study the Cosmic Microwave Background (CMB) map, which represents the remnants of the Big Bang. The CMB map provides a detailed snapshot of temperature fluctuations that are indicative of density variations in the early universe. Our approach aimed to uncover patterns or structures within these fluctuations using CA, a computational method well-suited for modeling complex systems that evolve over time according to simple rules.
We began by converting the CMB map into a form suitable for CA analysis. The map’s temperature variations were discretized into a set of states, which allowed us to represent different temperature bands as distinct numerical values. This step effectively translated the CMB data into a 2D grid, where each cell represents a localized temperature variation. By mapping these variations into a manageable number of states, we were able to apply CA rules to simulate the evolution of these states over time.
To analyze the transformed map, we applied a simple CA rule that adjusted each cell’s state based on the sum of its neighbors. This rule served as a way to simulate interactions between regions of different temperatures, effectively smoothing or amplifying certain patterns as the system evolved. After running a single iteration, we used the ABBA equation [A+B−][b−a+][b−a+][A+B−] to quantify the relationship between high and low state regions. In this context, states greater than 2 were considered “positive” (A+B) and those less than or equal to 2 as “negative” (b-a), allowing us to evaluate the balance between these areas in the transformed CMB map.
Further analysis involved iterating the CA model for multiple steps, allowing the simulated system to evolve and reveal more complex patterns. After five iterations, the CA produced a map with more pronounced clustering of higher states, suggesting an increasing dominance of these regions over time. The recalculated ABBA equation for this multi-step simulation indicated a shift in the ratio, reflecting changes in the spatial distribution of temperature bands as governed by the CA rules. This approach highlights the potential of using CA and mathematical equations like ABBA to study the emergent structures in the CMB data, providing a new way to explore the underlying dynamics of the early universe.
Overall, this process demonstrated how CA can be a valuable tool for analyzing complex astronomical data, offering insights into the evolution of the universe’s structure from initial fluctuations in the CMB. By applying iterative CA rules and quantifying changes with the ABBA equation, we were able to reveal patterns that may otherwise be challenging to discern, illustrating the power of computational methods in cosmological research.